Josephson energy
In superconductivity, the Josephson energy is the potential energy accumulated in the Josephson junction when a supercurrent flows through it. One can think about a Josephson junction as about a non-linear inductance which accumulates (magnetic field) energy when a current passes through it. In contrast to real inductance, no magnetic field is created by a supercurrent in Josephson junction --- the accumulated energy is a Josephson energy.
Derivation
For the simplest case the current-phase relation (CPR) is given by (aka the first Josephson relation):
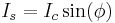
where 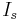 is the supercurrent flowing through the junction,
is the supercurrent flowing through the junction, 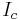 is the critical current, and
is the critical current, and 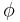 is the Josephson phase, see Josephson junction for details.
is the Josephson phase, see Josephson junction for details.
Imagine that initially at time 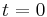 the junction was in the ground state
the junction was in the ground state 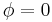 and finally at time
and finally at time  the junction has the phase
the junction has the phase  . The work done on the junction (so the junction energy is increased by)
. The work done on the junction (so the junction energy is increased by)
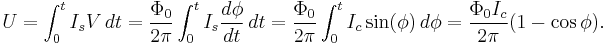
Here 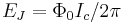 sets the characteristic scale of the Josephson energy, and
sets the characteristic scale of the Josephson energy, and 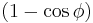 sets its dependence on the phase
sets its dependence on the phase  . The energy
. The energy 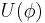 accumulated inside the junction depends only on the current state of the junction, but not on history or velocities, i.e. it is a potential energy. Note, that
accumulated inside the junction depends only on the current state of the junction, but not on history or velocities, i.e. it is a potential energy. Note, that 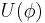 has a minimum equal to zero for the ground state
has a minimum equal to zero for the ground state 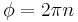 ,
,  is any integer.
is any integer.
Josephson inductance
Imagine that the Josephson phase across the junction is 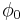 and the supercurrent flowing through the junction is
and the supercurrent flowing through the junction is
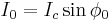
(This is the same equation as above, except now we will look at small variations in 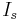 and
and 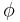 around the values
around the values 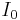 and
and 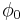 .)
.)
Imagine that we add little extra current (dc or ac) 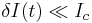 through JJ, and want to see how the junction reacts. The phase across the junction changes to become
through JJ, and want to see how the junction reacts. The phase across the junction changes to become 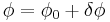 . One can write:
. One can write:
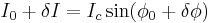
Assuming that 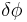 is small, we make a Taylor expansion in the right hand side to arrive at
is small, we make a Taylor expansion in the right hand side to arrive at
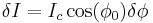
The voltage across the junction (we use the 2nd Josephson relation) is
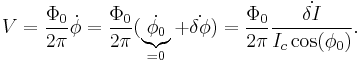
If we compare this expression with the expression for voltage across the conventional inductance
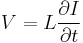 ,
,
we can define the so-called Josephson inductance
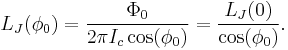
One can see that this inductance is not constant, but depends on the phase 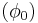 across the junction. The typical value is given by
across the junction. The typical value is given by 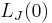 and is determined only by the critical current
and is determined only by the critical current 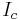 . Note that, according to definition, the Josephson inductance can even become infinite or negative (if
. Note that, according to definition, the Josephson inductance can even become infinite or negative (if 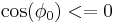 ).
).
One can also calcuate the change in Josephson energy
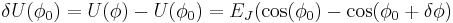 Making Taylor expansion for small
Making Taylor expansion for small 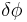 , we get
, we get 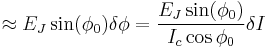
If we now compare this with the expression for increase of the inductance energy 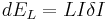 , we again get the same expression for
, we again get the same expression for 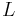 .
.
Note, that although Josephson junction behaves like an inductance, there is no associated magnetic field. The corresponding energy is hidden inside the junction. The Josephson Inductance is also known as a Kinetic Inductance - the behaviour is derived from the kinetic energy of the charge carriers, not energy in a magnetic field.